Db2 AVG

Summary: in this tutorial, you will learn how to use the DB2 AVG() function to calculate the average of a set of non-null values.

Introduction to Db2 AVG() function

The Db2 AVG() function is an aggregate function that returns the average of a set of values. Here is the syntax of the AVG() function:

AVG(expression)
Code language: SQL (Structured Query Language) (sql)

The AVG() function accepts a set of numeric values and returns the average of these numbers.

The data type of the return value depends on the data type of the input numbers. The AVG() function determines the data type of the return value based on the following rules:

• If the argument is DECFLOAT(n), the return type is DECFLOAT(34).
• If the argument is SMALLINT, the return type is BIGINT.
• If the argument is single precision floating-point, the return type is double precision floating-point.
• Otherwise, the return type is the same as the type of the argument.

The AVG() function returns NULL if the set is empty.

Note that the AVG() function ignores NULL values in the calculation.

Db2 AVG() illustration

First, create a new table named avg_demo that contains one integer column:

CREATE TABLE avg_demo(c1 INT);
Code language: SQL (Structured Query Language) (sql)

Second, insert four rows into the avg_demo table:

INSERT INTO avg_demo(c1) 
VALUES(1),(2),(3),(NULL);
Code language: SQL (Structured Query Language) (sql)

Third, view the data from the avg_demo table by using the following SELECT statement:

SELECT c1 FROM avg_demo;
Code language: SQL (Structured Query Language) (sql)

Fourth, use the AVG() function to return the average values in the c1 column of the avg_demo table:

SELECT 
    avg(c1) 
FROM 
    avg_demo;
Code language: SQL (Structured Query Language) (sql)

Here is the output:

AVERAGE     
----------- 
2       
Code language: SQL (Structured Query Language) (sql)

Behind the scenes, Db2 performs the following calculation:

• First, ignore the NULL values.
• Then, divide the sum of all values by the number of values (1+2+3) / 3 = 2.

Db2 AVG() examples

Let’s take some examples of using the AVG() function. We’ll use the books table from the sample database for the demonstration purposes.

1) Using DB2 AVG() function to calculate the average of values example

This example uses the AVG() function to calculate the average rating of all books in the books table:

SELECT 
    AVG(rating) avg_book_rating
FROM
    books;
Code language: SQL (Structured Query Language) (sql)

Here is the output:

AVG_BOOK_RATING
-------------------------------
4.00466544454628780934922089825
Code language: SQL (Structured Query Language) (sql)

To make the result more usable, you can use the CAST expression as follows:

SELECT 
    CAST(AVG(rating) AS DEC(4,2)) avg_book_rating
FROM
    books;
Code language: SQL (Structured Query Language) (sql)

Now the output is much much more readable:

AVG_BOOK_RATING
---------------
            4.00
Code language: SQL (Structured Query Language) (sql)

2) Using DB2 AVG() function with the GROUP BY clause example

The AVG() function is often used with the GROUP BY clause to find the average values of groups.

The following example returns the average rating of books by publishers:

SELECT 
    p.name publisher, 
    CAST(AVG(b.rating) AS DEC(4,2)) avg_rating  
FROM 
    books b
    INNER JOIN publishers p
        ON p.publisher_id = b.publisher_id
GROUP BY 
    p.name
ORDER BY avg_rating DESC;	
Code language: SQL (Structured Query Language) (sql)

This picture shows the partial output:

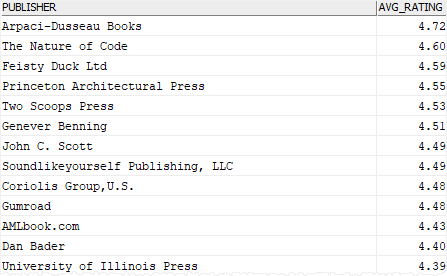
In this example, the GROUP BY clause groups rows by publishers and the AVG() function returns the average book rating for every group.

3) Using DB2 AVG() function with the HAVING clause example

This example returns the publishers whose average book ratings are higher than 4.5:

SELECT 
    p.name publisher, 
    CAST(AVG(b.rating) AS DEC(4,2)) avg_rating  
FROM 
    books b
    INNER JOIN publishers p
        ON p.publisher_id = b.publisher_id
GROUP BY 
    p.name
HAVING
    AVG(b.rating) > 4.5
ORDER BY avg_rating DESC;	
Code language: SQL (Structured Query Language) (sql)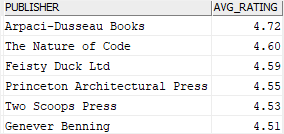

In this example, the HAVING clause includes only publishers whose average book ratings are greater than 4.5.

4) Using DB2 AVG() function with other aggregate functions example

The following example returns the average book rating and the number of books by publishers with a condition that the average book rating is higher than 4 and the number of books is greater than 10.

SELECT 
    p.name publisher, 
    CAST(AVG(b.rating) AS DEC(4,2)) avg_rating,
    COUNT(b.book_id) as book_count
FROM 
    books b
    INNER JOIN publishers p
        ON p.publisher_id = b.publisher_id
GROUP BY 
    p.name
HAVING
  AVG(b.rating) > 4 AND
  COUNT(b.book_id) > 10
ORDER BY 
  avg_rating DESC, 
  book_count DESC;
Code language: SQL (Structured Query Language) (sql)

Here is the output:

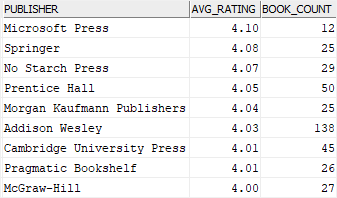
In this tutorial, you have learned how to use the Db2 AVG() function to calculate the average of a set of non-null values.